Особенности оптимизации толщины утеплителя наружных стен зданий. Системные аспекты

И. Н. Ковалев, доцент Института управления, бизнеса и права (Ростов-на-Дону)

Ю. А. Табунщиков, доктор техн. наук, проф., член-корреспондент РААСН

Отечественная экономика сейчас находится в преддверии очередной энергетической перегруженности, вызванной необходимостью вывода из работы большого количества неэффективных старых электростанций с низким КПД. Поэтому проблема энергосбережения и энергоэффективности не утратила актуальности, несмотря на инвестиционный рывок в электроэнергетике по итогам реформы 1998–2008 годов (тогда было введено более 30 ГВт мощностей электростанций и сопутствующей сетевой инфраструктуры). Да, грозивший еще 10 лет назад дефицит мощности был снят, но необходимость модернизации генерирующих мощностей опять предполагает значительные инвестиции. Инвестиции в энергосбережение, естественно, сопутствуют решению этих задач, снижая энергетические потребности.

Методическое обеспечение оптимизации соответствующих долгосрочных капиталовложений требует, прежде всего, узаконить давно обоснованные в мировой практике основные критерии: чистый дисконтированный доход (ЧДД) и индекс доходности (ИД), оставив сроку окупаемости инвестиций роль вспомогательного критерия.

Далее, следует внести ясность в назначение метода приведенных затрат – область его использования и, что даже более важно, предостеречь от неверного его толкования и применения. Нужно сказать, что большинство принципиальных положений экономических расчетов в плановой экономике (метод сравнения вариантов, приведенные затраты, учет неединовременности инвестиций и др.) остались неизменными и в рыночных условиях, но все узловые моменты приобрели теперь нелинейный характер. Эта нелинейность предполагает большее творческое участие лиц, принимающих решения, по сравнению с линейной плановой экономикой, где все было однозначно, включая назначенные государственные цены.

СПРАВКА;

В соответствии с научно обоснованной методологией определения требуемого сопротивления тепло­передаче наружных ограждающих конструкций его величина должна определяться в соответствии с двумя этапами: первый этап – сопротивление теплопередаче должно быть не менее величины, требуемой по санитарно-гигиеническим условиям; на втором этапе величина сопрот Такая логичная методология определения теплозащиты наружных ограждающих конструкций была принята в СНиП II-3–79 «Строительная теплотехника». Игнорирование этой методологии приводит к серьезным ошибочным результатам. Так, например, в СНиП II-3–79* «Строительная теплотехника» (СНиП 1999 года) был проигнорирован указанный выше подход к определению требуемого сопротивления теплопередаче и была принята методология определения требуемого сопротивления теплопередаче в зависимости от градусо-суток отопительного периода. Из статьи Ю. А. Табунщикова «В поисках истины», журнал «АВОК» № 6, 2014

Довольно неспокойное развитие нашей полит­экономики обязывает непрерывно совершенствовать используемые математические модели в сторону их гибкости для получения обоснованных решений в условиях частого, неожиданного и сильного изменения характера всевозможных неопределенностей. Пути их преодоления известны и основаны на многовариантных расчетах. Поэтому в самом общем виде расчетные алгоритмы можно представить в двухслойном виде.

Первый слой – математическая модель функциональной зависимости «выхода» расчета от заданного «входа», чаще всего в детерминированном виде и обычно довольно простая. Это оператор – ядро алгоритма.

Рисунок 1. Приведенные затраты при дополнительном утеплении ограждающей конструкции

Второй слой – многовариантные расчеты с помощью этого аналитического ядра по определенным сценариям, составленным в том числе с помощью экспертных процедур.

Затронутые вопросы рассмотрены в настоящей работе на простом примере экономической оптимизации толщины утеплителя наружных стен зданий. На основе соответствующей экономической модели в заключение дается таблица с усредненными толщинами утеплителей для всех регионов РФ с учетом уже установленных по санитарно-гигиеническим условиям и иным, в соответствии с действующими законодательными документами.

Математическая модель оптимизации

В качестве примера двухслойного подхода рассмотрим задачу оптимизации толщины утеплителя наружных стен здания при допущении их однородности. Соответствующая математическая модель используется многими авторами [1–4] и сводится к составлению целевой функции вида (1) (см. Формулы).

РАСЧЕТНЫЕ ФОРМУЛЫ

В качестве исходной величины сопротивления теплопередаче может быть принята величина, определяемая в соответствии с СП 50.13330.2012 «Тепловая защита зданий» или принятая по санитарно-гигиеническим требованиям (см. Послесловие).

Приведенные затраты (1) составлены при условии инвестирования собственных средств предприятия в утеплители. Ниже будет обосновано данное упрощение, позволяющее не учитывать возможность заемных средств и соответствующий леверидж.

Определяем оптимальную толщину дополнительного утеплителя, дифференцируя (1) по переменной δ_Э и приравнивая полученное уравнение к нулю (2).

Решая квадратное уравнение, получаем результат (3).

Полученное решение, как видим, имеет две независимые составляющие. Первая составляющая – это экономически целесообразная толщина Δ_Э однослойного утеплителя вне зависимости от возможного наличия некоторого первоначального слоя толщиной δ₀. Именно поиску этой величины посвящены работы [1, 5]. Наличие же первоначального слоя, установленного по ряду внеэкономических соображений (см. выше и Послесловие), оказывается де-факто заведомо экономически целесообразно, если Δ_Э > δ₀. Если бы оказалось, что Δ_Э < δ₀, следовало бы принять Δ_Э = 0 и утверждать, что имеющийся теплоизоляционный слой не оправдывает экономического «усиления». Однако, как показали расчеты (табл. 2), реальность далека от такого тривиального решения.

Ниже будет показано, что суммарная величина

Δ_Э = δ_Э + δ₀ и соотношение ее составляющих дает полную информацию об экономической эффективности полученного решений, эти две величины определяют численные значения критериев ДД, ЧДД, ИД, Т_о и Т_ок (см. ниже) и нет необходимости обращаться к исходной модели (1) для их расчета.

Рисунок 2. Диаграмма денежных потоков при использовании утеплителя

Пример расчета

В качестве иллюстрации рассмотрим условный регион со значением ГСОП, равным 8 000 ⁰C•cут. Стоимость тепловой энергии С принята 3 000 руб./Гкал, что приближено к реальным тарифам на электроэнергию. Остальные технико-экономические показатели принимаются равными¹: К = 2 500 руб./м³, Е = 0,15 1/год, Т_эн = 2,8, R₀ = 3,3 м²•°C/Вт, λ = 0,04 Вт/м•°C. Средний уровень перспективной инфляции принят i = 7,5 %, соответствующая норма дисконта будущих доходов от работы утеплителей r = 2i = 15 %.

Принятое численное значение для коэффициента Е = r = 0,15 будет обосновано позже.

Толщина утеплителя согласно (3) рассчитывается по формуле (4).

На рис. 1 этому решению отвечает точка А на кривой 3 приведенных затрат. Здесь же показана кривая 2 снижения энергопотерь ΔW(δ) благодаря установке искомого утеплителя и прямая роста 1 приведенных инвестиций К•δ_Э•Е на его установку. Очень важный показатель

ΔΔW = ΔW₀ – ΔW_δЭ, руб./м² •год – стоимость снижения тепловых потерь на 1 м² утеплителя в год. Обозначим этот годовой доход как Д. Формулу для его расчета найдем, используя второе слагаемое в затратах (1) дважды – до установки утеплителя и после (5).

Принимая, что R₀•λ ≈ δ₀, и освобождаясь от громоздкого первого сомножителя в (5) с помощью соответствующей подстановки из (3), получаем компактную формулу (6).

Сопоставление этого эффекта с затраченными инвестициями к на 1 м² утеплителя (7) определит эффективность данного мероприятия. Найдем соответствующие экономические показатели согласно [1].

Суммарный дисконтированный доход за срок Т службы утеплителя определяется по формуле (8) или (9).

Расчет этого показателя проведем иначе, через посредство найденных оптимальных параметров утеплителя. Представляя квадратную скобку усредненной величиной 0,95 (или принимая ее за единицу) и учитывая (6), получаем упрощенную формулу (9), дающую практически тот же результат.

Чистый дисконтированный доход определяем по формуле (10).

Используя упрощенную формулу (9), ЧДД можно рассчитывать по формуле (11).

Индекс доходности по точной формуле (10) определяем в соответствии с (12) или же с использованием упрощенной формулы (11) в соответствии с (13).

Рассчитанный ИД свидетельствует о получении через 20 лет на каждый вложенный рубль доход 1 руб. 75–80 коп.

При этом фактор инфляции уже учтен посредством нормы дисконта.

В качестве дополнительного критерия эффективности определим срок окупаемости инвестиций к с учетом дисконта получаемых ежегодных доходов Д. Соответствующая известная формула [1] предполагает знание простого (бездисконтного) срока окупаемости Т₀. Соответствующую формулу найдем с помощью (6) и (7) или (11) и (7) по формуле (14).

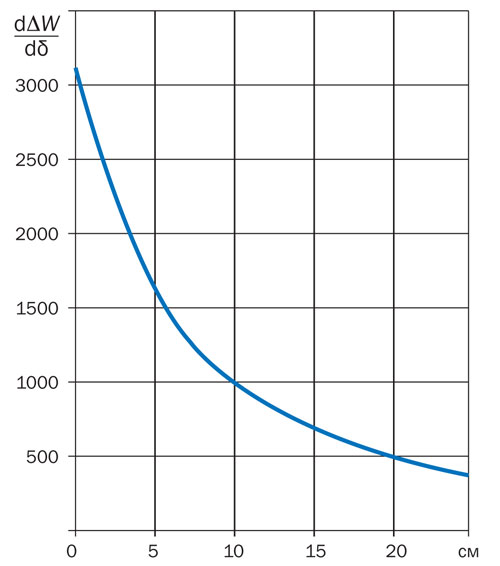Рисунок 3. Снижение эффекта «последней порции» утеплителя

Теперь найдем срок окупаемости с учетом дисконтирования доходов по формуле (15).

На рис. 2 показана кривая дисконтированного дохода и все найденные экономические показатели нашего примера. Заметим, что приведенные упрощенные формулы для расчета экономических показателей работы инвестиций дают погрешность, как правило, не более 10 %, что в условиях высоких неопределенностей в работе долгосрочных инвестиций следует признать допустимым.

Специфические особенности расчетного алгоритма

Второй слой алгоритма, как уже было сказано, связан с учетом значимых факторов целевой функции, обусловленных их особенностями и обстоятельствами эксплуатации оборудования в условиях неопределенности.

К внутренним (эндогенным) факторам системы отнесем теплофизические параметры R₀ и λ, климатический индекс ГСОП, стоимость утеплительного материала К. Внешние (экзогенные) факторы – это стоимость энергии С и экономический показатель Е приведения инвестиций к одному году. Численные показатели этих факторов определяются энергетической политикой государства, в том числе на международном уровне. Неопределенность здесь значительно выше, чем в ряде эндогенных переменных (особенно это относится к величине Е, зависящей от инфляции и от дефицитности инвестиционного материала). Дополнительная сложность определяется тем, что в рассматриваемой модели переменные С и Е должны присутствовать своими прогнозируемыми усредненными значениями на всем временнoм интервале Т эксплуатации утеплителя (см. ниже).

Но прежде всего поясним возможность не учитывать леверидж, если он реально присутствует в варианте кредитования инвестиций, целиком или частично. Большинство энергосберегающих мероприятий представляют собой процессы с двумя удобными для расчета особенностями:

• во-первых, длительный срок службы (десятилетия),
• во-вторых, довольно стабильный во времени годовой сберегающий эффект.

Это и позволяет существенно упростить задачу экономической оценки их работы, а именно – условно считать, что все 100 % инвестиций обеспечиваются собственными средствами. Иными словами, леверидж не оказывает влияния на эффективность применения энергосберегающих устройств.

Это непосредственно следует из теории Ф. Модильяни и М. Миллера [6]. Но если в общем случае теория предусматривает оговорки, связанные со спецификой функционирования финансовых и фондовых рынков (различные проценты и налоги), то отмеченные выше особенности энергосбережения выводят эти оговорки за скобки. Справедливость данного упрощения обоснована и проиллюстрирована графически в [5]. Заметим, что эта закономерность следует из тождества (16), уравнивающего сроки окупаемости инвестиций, реализованных на собственные средства и целиком на заемные.

Из выражения (15) или (16) следует постулат, что необходимым условием окупаемости является неравенство  (17).

Однако на практике это условие малопродуктивно, поскольку обычно добиваются «быстрой» окупаемости, приносящей впоследствии заметный доход. Но величина такого значимого дохода предполагает существенное отступление величины (Т₀• r) от 1. Так, можно утверждать: достаточным условием выгодных инвестиций служит неравенство (18), которое обеспечивает ИД ≥ 0,35. Если лица, принимающие решения, претендуют, например, на ИД ≥ 0,5, то в этом случае должно выполняться неравенство Т₀• r ≤ 0,63.

Предназначение приведенных затрат

Вернемся к анализу приведенных затрат. Прежде всего

рассмотрим их прямое функциональное назначение, выясняя попутно возможные заблуждения в части иных вариантов их использования.

Основные преимущества приведенных затрат:

• удобство экономического сравнения большого числа конкурентных вариантов инвестиций;
• удобство поиска оптимальных значений параметров проектируемой системы при их непрерывном изменении (толщина утеплителя, сечение проводов линий электропередач, оптимальная мощность энергоустановок и т. д.).

Основным регулятором в приведенных затратах при расчетах является коэффициент приведения E, на который в плановой экономике воздействовали государственные органы, что делало пользование этой величиной тривиальным, равно как и пользование постоянными ценами. В нынешней же относительно рыночной экономике страны коэффициент Е предполагает творческий подход  лиц, принимающих решения. Задавая допустимый срок окупаемости инвестиций Т_ок или минимальный ИД, лица, принимающие решения, влияют на экономическую эффективность инвестиций, на уровень их отдачи.

Понижая величину Т_ок и повышая величину ИД, стремятся уменьшить инвестиции при одновременном росте их удельного эффекта, что логично при снижении инвестиционного потенциала, и наоборот. При этом точка А (рис. 1) смещается влево. В этом – единственное функциональное предназначение приведенных затрат.

Но часто делаются попытки «двигать» точку А вправо или влево не через осознанное соответствующее воздействие на показатель Е, но опираясь на некие интуитивные представления, что неизбежно ведет к отступлению от верных ориентиров. При этом такой произвол оправдывают, например, тем, что гипербола 2 (рис. 1) вначале якобы убывает быстро, а затем становится пологой. Это впечатление обманчиво. В случае гиперболических кривых относительное приращение абсциссы приблизительно равно убыванию ординаты. В экономике это формулируют как приближение ценовой эластичности гиперболы (обычно ею представляется кривая спроса) к единице.

Таким образом, главное и практически единственное предназначение приведенных затрат – искать их экстремум с последующим практическим приближением к найденной точке, преодолевая многозначность факторов и их неопределенность. В любом случае следует рассматривать две кривые приведенных затрат (гиперболу и прямую линию инвестиций) совместно, не пренебрегая математической обоснованностью решений.

Коэффициент приведения в «непрерывной» задаче оптимизации

Оптимизационная задача с непрерывно варьируемым аргументом (в нашем случае параметр δ_Э) имеет определенную специфику по назначению величины коэффициента приведения Е в формуле (1), в отличие от варианта с неделимостью инвестиций. Рассмотрим ее подробнее.

В плановой экономике критерием выгодности дополнительных инвестиций был, как известно, бездисконтный (простой) срок их окупаемости Т_н. При этом «коэффициент эффективности капиталовложений» рассчитывался просто: Е_н = 1/Т_н.

Обоснование даже такого несложного линейного подхода потребовало недюжинных усилий со стороны автора концепции, ученого-экономиста В. В. Новожилова [7]. В условиях тотальной плановой экономики только так оказалось возможным как-то определять путь к поиску «глобального оптимума» государственных капиталовложений при распределении фондов между отраслями, крупными предприятиями и т. д. Переход к рыночным (нелинейным) методам предопределил учет фактора процента, а в части оценки эффективности инвестиций – фактора дисконта, выражаемого величиной r. Сейчас сформировалось два подхода к определению экономического показателя приведения Е [1, 4, 5]:

• при нормировании срока окупаемости Т_ок ≤ 5 лет применяется формула (19);
• при нормировании индекса доходности инвестиций ИД применяется формула (20).

Но в случае задачи с непрерывно изменяемым параметром (например, толщина утеплителя) мы сталкиваемся с необходимостью задаваться величинами ИД или Т_ок, относящимися к «последней порции» (ПП) определяемого параметра, в соответствии с классическим методом поиска экстремума целевой функции (2). Именно так обстояло дело при создании формул (1)–(3).

Важно то, что проектировщика интересует ИД или Т_ок по работе устройства энергосбережения в целом, с учетом всех его «порций», от первой до последней. Чтобы обосновать коэффициент Е для ПП, воспользуемся упорядоченностью эффектов (снижение тепловых потерь) от первой до последней «порции», а именно: максимум от первой «порции» и минимум от последней, в промежутке – снижение эффекта по гиперболе (2) (рис. 1).

Перейдем к цифрам. Для рассмотренного примера эффект «первой порции» рассчитан согласно второму слагаемому формулы (2) при δ_Э = 0 и равен 3 085 руб./м³•год. Эффект же «последней порции» снижается до 375 руб./м³ •год. Разрешить ситуацию можно так. Эффект «последней порции» не так и важен, поэтому величина Е в формуле (1) может быть рассчитана при ИД = 0 или, что эквивалентно, Т_ок → ∞. И тогда согласно формулам (19) и (20) для показателя Е получаем значение (21), что и принято выше при рассмотрении модели утеплителя. На рис. 3 показана гипербола снижения эффектов от первой «порции»  до последней, что рассчитывалось по второй составляющей формулы (2) при условии 0 ≤ δ_Э≤ 0,25 м.

Расчетно-прогнозные цены на энергоносители

Следующий важный момент связан с долгосрочностью энергосберегающих инвестиций в условиях неустановившейся экономики. Принимая сейчас решения, нужно каким-то образом учитывать стоимость С энергии (тепловой или электрической) с учетом тарифного (или сугубо рыночного) роста на длительных интервалах работы объектов. При однородной инфляции проблемы бы не возникло, поскольку в расчетах участвует, как правило, отношение С/К (см. формулу (3)).

Но применительно к России такой однородности еще долгое время не будет, а вынужденно будет выдерживаться «догоняющий» рост энергетических тарифов [5], примерно в полтора-два раза превышающий общую инфляцию. Это дает впечатляющий рост стоимости энергии относительно инфляции. Так, за 20 лет при ежегодном наращении 15 % и общей инфляции 7 % получаем относительный рост стоимости  энергии в 16 с лишним раз. Возникает вопрос – какую стоимость принимать в расчетах?

Корректировать стоимость энергии в процессе эксплуатации немыслимо, принятое ошибочное решение изменить нереально. Напрашивается рекомендация использовать среднюю прогнозную стоимость за срок Т, поскольку иные варианты менее обоснованны. Соответствующая формула для среднего значения тарифа с использованием для простоты записи представлена в показательной форме [5] согласно (22).

Составляя аналогичное уравнение для динамики цены на утепляющие материалы с учетом соответствующей усредненной инфляции ik и взяв отношение первого уравнения ко второму, получаем уравнение (23) для расчета  искомого тарифного коэффициента Т_эн.

В табл. 1 приведены значения Т_эн для различной базовой инфляции при условии удвоения тарифных ставок на энергоносители и полуторном их увеличении.

Отсюда видно, что и при умеренной инфляции, и при невысоком опережающем росте энергетических тарифов поправка на стоимость С значительна и ее нужно учитывать.

Анализ результатов расчета утеплителей для регионов

Толщины дополнительных утеплителей зданий δ_Э для регионов РФ (табл. 2) рассчитаны по формуле (3), исходя из достижения их максимальной экономической эффективности – минимизации целевой функции приведенных затрат вида (1). При этом для всех регионов была принята единая цена тепловой энергии С = 2500 руб./Гкал. Тарифный коэффициент принимался в расчете на умеренную инфляцию: Т_эн = 1,4 (табл. 1). Пересчет величин δ_Э в соответствии с реальной ценой С_i для конкретного региона нужно вести  по формуле (24).

Таблица 1 Значения ТЭ для различной базовой инфляции

при увеличении тарифных ставок на энергоносители в 2 раза iβ, % 2.5 5 7.5 10 Iк, % 5.0 10 15 20 ТЭН 1.3 1.9 2.8 4.2 при увеличении тарифных ставок на энергоносители в 1,5 раза Iк, % 2.5 5 7.5 10 Iк, % 3.8 7.5 11.3 15 ТЭН 1.2 1.4 1.6 2.0

Поскольку величина простого срока окупаемости Т₀ участвует в определении срока окупаемости инвестиций Т_ок, она рассчитывалась в первую очередь по формуле (14). По формуле вида (15) определялся срок окупаемости Т_ок и по формуле (13) – индекс доходности инвестиций (ИД) в дополнительные утеплители.

Таблица 2 Толщина дополнительного слоя утеплителя для некоторых регионов Российской Федерации

Из табл. 2 следует, что экономически оптимально для всех регионов увеличить толщины имеющихся утеплителей примерно в полтора раза. Соответствующие инвестиции окупаются в интервале 6–8 лет при стабильном индексе доходности в диапазоне 0,5–0,7. Все это обнаруживает рациональность дополнительного утеплительного процесса при ощутимой экономической эффективности.  Последнее существенно ниже, чем в рассмотренном выше числовом примере, поскольку стоимостные энергетические показатели снижены в 2,5 раза. Возвращаясь к рис. 3, констатируем, что найденные дополнительные утеплители, успешно снижая потери в нижней части гиперболической кривой, дополняют еще более экономически оправданный процесс уже установленной ранее теплоизоляции.

Послесловие

1. В данной статье при расчете экономически целесообразного сопротивления теплопередаче наружных стен авторы за исходную величину для расчетов принимали сопротивление теплопередаче наружных стен в соответствии с СП 50.13330.2012 «Тепловая защита зданий». Представляется, что методически правильно за исходную величину сопротивления теплопередаче принимать его величину, рассчитанную по санитарно-гигиеническим условиям, а затем проводить расчеты экономически целесообразного сопротивления теплопередаче по методике, изложенной в статье. Однако, как показали проведенные нами расчеты, величина экономически целесообразного сопротивления теплопередаче не зависит от исходной величины, принятой по санитарно-гигиеническим условиям или в соответствии с СП 50.13330.2012 «Тепловая защита зданий».

2. Для того, чтобы методика расчетов приобрела закономерно-нормативный характер, необходимо на правительственном уровне для экономических расчетов утвердить расчетную величину инфляции на период по крайней мере 5–7 лет и расчетную величину стоимости тепловой энергии.

Литература

1. Дмитриев А. Н., Ковалев И. Н., Табунщиков Ю. А., Шилкин Н. В. Руководство по оценке эффективности инвестиций в энергосберегающие мероприятия. М. : АВОК-Пресс, 2005.
2. Гагарин В. Г. Методы экономического анализа повышения уровня теплозащиты ограждающих конструкций зданий // АВОК. 2009. №№ 1–3.
3. Горшков А. С. Об окупаемости инвестиций на утепление фасадов существующих зданий // Энергосбережение. 2014. № 4.
4. Ковалев И. Н. Инвестиционная оптимизация технических систем с непрерывно изменяемыми параметрами при проектировании // Энергосбережение. 2013. № 6.
5. Ковалев И. Н. Рациональные решения при экономическом обосновании теплозащиты зданий // Энергосбережение. 2014. № 8.
6. Модильяни Ф., Миллер М. Сколько стоит фирма. М. : Дело, 2001.
7. Экономическая школа (периодический научно-популярный журнал). – Предприятие «Экономическая школа» С.-Петербургского Университета экономики и финансов.  1992. Вып. 2. С. 7–14.
8. Табунщиков Ю. А. В поисках истины // АВОК. 2014. № 6. С. 4.

¹ В примере принята величина R₀, которая соответствует ГСОП, равной 5 000 °С•сут. Как будет отмечено в Послесловии, выбор исходной величины (отправной точки для расчетов) не влияет на конечный результат.