Теплотехнический расчет спортивного катка с накладными металлическими элементами

М. А. Гуревич, канд. техн. наук;

Ю. А. Табунщиков, доктор техн. наук

В мировой практике строительства спортивных помещений многоцелевого назначения наиболее привлекательным вариантом спортивного катка является такой его вид, когда он выполнен трансформируемым, т. е. спортивное помещение представляет собой совмещение спортивного катка и легкоатлетического манежа.

В легкоатлетическом манеже полом является синтетическое покрытие, уложенное по асфальтобетону. Намораживание (сезонное, в течение 5 месяцев) производится на специальные элементы, шаблон из стали с трубками, укладываемые поверх синтетического покрытия. Такой каток мы в дальнейшем будем называть искусственным спортивным катком с накладными металлическими элементами.

Конструктивно это представляется следующим образом (рис. 1а): на синтетическое покрытие легкоатлетического манежа (3) укладываются металлические панели (1) со впадинами и выступами, в которые помещаются сваренные в длинные плети циркуляционные трубы (2). По трубам циркулирует хладоноситель, обеспечивающий намораживание льда. Монтаж предложенного устройства производят в следующем порядке. В направлении, перпендикулярном размещению труб (2), металлические панели (1) соединяют внахлест, а в продольном направлении пристыковывают с применением скоб (4) (рис. 1б). Затем сваренные в длинные плети циркуляционные трубы (2) укладывают во впадины панелей (1). Применение данного устройства для искусственных спортивных катков позволяет обеспечить необходимую герметичность и жесткость системы, упростить ее сборку и разборку и достичь более равномерного распределения температур по поверхности льда. Известно устройство для намораживания ледяного поля переносного искусственного катка, включающее плиты из материала с хорошей теплопроводимостью и систему труб для прохождения хладоносителя, прикрепленные к металлическим балкам специального профиля [1], [2]. Известно также другое устройство для намораживания ледяного поля трансформируемого искусственного катка, содержащее металлические панели и имеющее с ними тепловой контакт трубы для циркуляции хладоносителя [3]. Недостатком указанных устройств является относительно большой вес и сложность монтажа и разборки из-за наличия значительного количества сборных элементов.

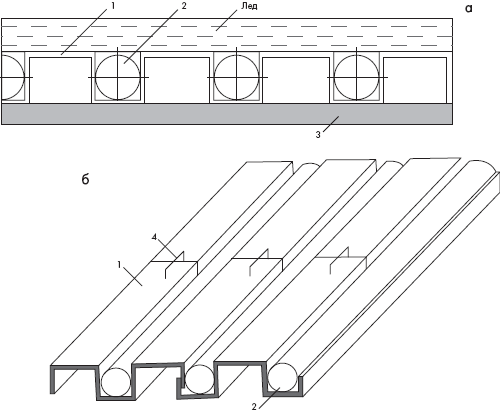Рисунок 1. а – схема устройства для намораживания ледяного поля трансформируемого искусственного катка; б – фрагмент устройства при монтаже

Предлагаемое в статье устройство для намораживания ледяного поля трансформируемого искусственного катка, содержащее металлические панели и имеющее с последними тепловой контакт трубы для циркуляции хладоносителя, отличается тем, что с целью обеспечения равномерного распределения температуры по поверхности льда и упрощения монтажа металлические панели имеют продольные впадины и выступы, а трубы смонтированы во впадинах панелей. На данное устройство получено авторское свидетельство № 577368.

Теплотехнический расчет катка с накладными металлическими эле-ментами заключается в решении двух основных задач:

1) Определение температуры охлаждающей среды в трубах (под слоем льда), обеспечивающей заданную рабочую температуру на поверхности льда, причем расстояние между трубами необходимо выбрать таким образом, чтобы максимальная неравномерность температур на поверхности льда не превышала 0,25 °С [1].

2) Расчет толщины заданной теплоизоляции охлаждающей плиты катка для предохранения нижележащих слоев грунта от промерзания, а также от возможного пучения грунта и разрушения основания катка.

Для решения первой основной задачи необходимо определить двухмерное стационарное поле температур основания катка, создаваемое трубами, по которым течет охлаждающая смесь [4]. Математически задача определения стационарного температурного поля сводится к нахождению функции t (x > y), удовлетворяющей уравнению теплопроводности в соответствующей области и граничным условиям на поверхности труб:

t (x,y) = t_T, (1)

на поверхности льда:

–l •∂t/∂y + a_в [t (x, y) – t_в] = 0, (2)

где t – температура, °С; t_T – температура на поверхности труб, °С.

Задача решалась при следующих допущениях: труба представляет собой бесконечно длинный цилиндрический источник тепла с диаметром, равным наружному диаметру трубы; температура наружной поверхности трубы t равна температуре охлаждающей смеси t_p, поскольку сопротивление теплоотдачи от охлаждающей смеси к стенке трубы и термическое сопротивление стенки металлической трубы малы, и ими можно пренебречь (теплофизические характеристики материалов катка не зависят от температуры, поэтому при решении задачи можно использовать линейное уравнение теплопроводности). Тепловыми потоками, поступающими из грунта к основанию катка, можно пренебречь [5, 6] ввиду их малой величины – они не превышают 7,6 Вт/м².

При расчете температурного поля спортивного катка с накладными металлическими элементами по программе расчета двумерных температурных полей приняты следующие исходные данные.

Слои материалов катка и их теплофизические характеристики (считая сверху вниз):

• лед толщиной d_л = 0,025 м с коэффициентом теплопроводности l_л = 2,3 Вт/(м • °С);

• воздушная прослойка между трубами с коэффициентом теплопроводности в направлении оси координат «X» l_x = 0,02 Вт/(м • °С); в направлении оси «Y» l_y= 0,13 Вт/ (м • °С) – по табл. 4 СНиП П-А.7-71;

• синтетическое покрытие (резиновая крошка на синтетическом связующем) g = 690 кг/м³, d_с.п = 0,015 м, l_с.п. = 0,13 Вт/(м • °С), удельной теплоемкостью С_с.п = 1,38 кДж/ (кг • °С);

• асфальтобетон, g = 2 100 кг/м³, d_а.б = 0,1 м, l_а.б = 1,05 Вт/(м • °С), С_а.б = 1,68 кДж/(кг • °С);

• теплоизоляция (керамзитовый гравий), g = 600 кг/м³, l_т.н = 0,20 Вт/ (м • °С), С_т.н = 0,84 кДж/(кг • °С);

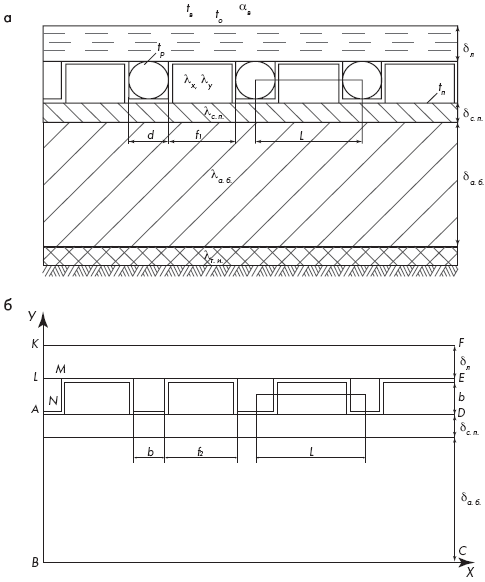Рисунок 2. Поперечное сечение катка с накладными металлическими элементами (а) и расчетная схема (б)

Накладной металлический элемент – шаблон из стали толщиной 2 мм с трубами диаметром d = 32 мм; температура воздуха в манеже t_в = 16 °С; средняя теплоотдача у поверхности льда, граничащей с воздухом (для закрытых помещений), a_в = 10,5 Вт/(м² • °С) [4]; рабочая температура на поверхности льда составляла –1,5; –2,5; –5 °С. На рис. 2б представлена расчетная схема искусственного катка. Цилиндрические трубы диаметром d на расчетной схеме заменены трубами квадратного сечения, периметр которого равен длине окружности поперечного сечения цилиндрической трубы; сторона квадрата принимается равной:

b = 1/4 pd. (3)

Расстояние между центрами квадратных сечений труб на расчетной схеме (с учетом масштаба) равно расстоянию между центрами круговых сечений труб на реальном катке. В соответствии с ранее принятыми допущениями, потоки тепла q_x через участки границы области AB, CD, EF, KL и q_y через участок BC равны нулю.

Задавая условия теплообмена на всех участках внешней границы расчетной области катка и температуру t⁰_y по контуру квадратных сечений, соответствующих трубам, можно рассчитать температуру t_л на поверхности льда. На основе данных таких расчетов определялась температура, которую должна иметь охлаждающая среда t_p в трубах (под слоем льда), чтобы обеспечить заданную рабочую температуру на поверхности льда t_л искусственного катка.

Для определения оптимальных характеристик катка с накладными металлическими элементами при расчетах варьировались следующие параметры: расстояние между трубами f; толщина синтетического покрытия d_с.п.; температура внутреннего воздуха t_в; температура на поверхности льда t_л; коэффициент теплопроводности прослойки между трубами l_пр. (рассматривалась возможность заполнения воздушной прослойки теплоизоляционным материалом). Результаты расчетов по различным вариантам приведены в таблице.

Температура поверхности льда изменяется синусоидально. Точка минимального значения t’_л располагается под центром каждой трубы, максимальная температура t’’_л льда отмечается в точке, равноотстоящей от двух соседних труб. Разность температур Dtл = t’_л – t’’_л называется максимальной неравномерностью температур поверхности льда.

Анализ данных таблицы позволяет сделать следующие выводы:

1. Для достижения рабочих температур (максимальных) на поверхности льда катка с накладными металлическими элементами t_л, равных –1,5; –2,5; –5 °С, температура охлаждающей смеси в трубах tp должна иметь, соответственно, значения –4; –5,1; –8 °С (при t_в = 16 °С; f₁ = 0,05 мм; d = 32 мм).

2. Оптимальным расстоянием между трубами, при котором надежно обеспечивается условие

D_tл < 0,25 °C, (4)

является 0,05 м.

3. При увеличении температуры внутреннего воздуха в помещении на 4 °С (от 16 до 20 °С) температура охлаждающей смеси в трубах t_p для получения заданной рабочей температуры на поверхности льда должна быть понижена на 0,5 °С.

4. Максимальная неравномерность температуры на поверхности льда Dt_л растет с увеличением температуры воздуха в помещении и расстояния между трубами f₁.

5. Заполнение воздушных прослоек между трубами теплоизоляционным материалом (пенополиуретан), g =75 кг/м; l = 0,042 Вт/ (м • °С), не дает теплотехнического эффекта.

6. Уменьшение толщины синтетического покрытия почти в 2 раза (от 0,015 до 0,008 м) практически не изменяет температурное поле в районе накладного металлического элемента искусственного катка.

Перейдем к решению второй основной задачи – определим толщину слоя теплоизоляции (керамзитовый гравий) под основанием катка, обеспечивающую непромерзание грунта под ним. Для этого необходимо рассчитать квазистационарное температурное поле основания катка, а также температурное поле грунта под основанием катка.

Математическая задача о расчете одномерного квазистационарного температурного поля основания катка и грунта под ним сводится к определению функции t (х, t), удовлетворяющей уравнению теплопроводности в рассматриваемой области и граничным условиям:

• на поверхности синтетического покрытия;

• в течение 5 месяцев года, когда манеж используется под каток,

t = t_n; (5)

• в течение остальных 7 месяцев, когда манеж используется для легкоатлетических соревнований,

–l_с.п. • ∂t/∂x + a_в [t (х, t) – t_в] = 0; (6)

• на плоскости, выделенной в грунте и расположенной на глубине l = 10 м [6], t = 6,5 °С.

В равенстве (5) t_n = –8,5 °С. Это минимальное значение температуры на поверхности синтетического покрытия t_в = 20 °С и температуры на поверхности льда t_л = –5 °С (указанное минимальное значение температуры получено при решении первой основной задачи).

В формуле (6) a_в = 10,5 Вт/ (м • °С) коэффициент теплоотдачи у поверхности синтетического покрытия, граничащего с воздухом; t – время, ч.

При расчете использовались теплофизические характеристики грунта, обладающего способностью к сильному пучению (пылеватый суглинок): объемный вес скелета грунта g_ск = 1 600 кг/м³, коэффициент теплопроводности l = 1,8 Вт/ (м • °С), объемная теплоемкость C • g_ск = = 2 948 кДж / (м³ • °С).

Результаты расчета температурного поля в поперечном сечении катка и в слое грунта показали, что теплоизоляция (керамзитовый гравий) толщиной 0,4 м под основанием катка с накладными металличес-кими элементами обеспечивает непромерзание грунта под ним.

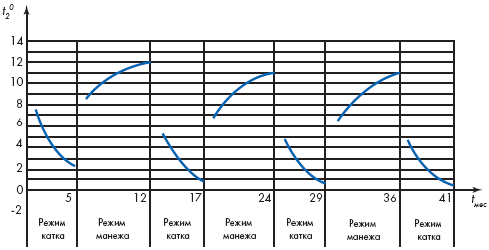Рисунок 3. График изменения температуры грунта на границе с теплоизоляцией

Таблица (подробнее) К определению оптимальных характеристик катка

Литература

1. Рекомендации по проектированию инженерного оборудования искусственных катков (хладотехническая часть). ЛенЗНИИЭП Госгражданстроя СССР. Л., 1972.

2. Холодильная техника: Энциклопедический справочник . Госторгиздат, 1961. С. 378–380.

3. Гиполин И. и др. Сборный каток из алюминиевых листотрубках панелей // Холодильная техника. 1960. № 1. С. 11–14.

4. Лихтенштейн Э. Л. Исследование температурного поля искусственного катка. Автореферат диссертации на соискание степени канд. техн. наук. Новосибирск, 1970.

5. Billington N.S. Floor – panel heating – some design data. J. of the Institution of heating and ventilating engineers. 1983, v 21, October.

6. Лукьянов B. C., Головко М. Д. Расчет глубины промерзания грунтов. М.: Трансжелдориздат, 1957.